domingo, 3 de janeiro de 2010
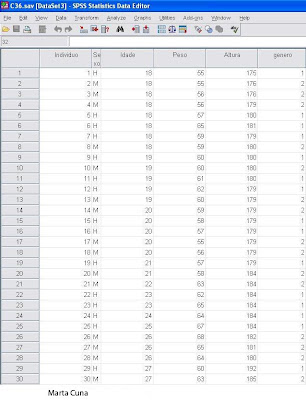
C.8 - Seleccionar amostras e gerar tabelas de números aleatórios.
Amostragem aleatória- Neste tipo de amostra a premissa é de que cada componente da população estudada tem a mesma chance de ser escolhido para compor a amostra e a técnica que garante esta igual probabilidade é a seleção aleatória de individuos, por exemplo através de sorteio.
Fonte:http://www.lee.dante.br/pesquisa/amostragem/planoamostral.html
Amostragem Sistemática- Deve obedecer o mesmo princípio da amostragem aleatória simples de iguais probabilidades de pertencer à amostra para todos os componentes da população estudada. No entanto, prevê a coleta de dados ao longo de um período de tempo e arbitra um ritmo para tomada de unidades da população para compor a amostra. Por exemplo, numa listagem de indivíduos da população, sorteamos um nome entre os dez primeiros da lista. A partir do nome sorteado, selecionamos um a cada dez indivíduos (o décimo, vigésimo e assim por diante). A aleatoriedade só está garantida se a apresentação de casos for também aleatória (exemplo: numa população de atendimentos médicos ambularoriais toma-se para amostra 1 em cada 10 pessoas que se apresentam para consulta médica. A amostra será aleatória se a apresentação de pacientes puder ser assumida como igualmente aleatória).
A amostragem sistemática é utilizada quando se quer planejar um período de tempo para execução da coleta de dados ou quando se deseja cobrir um determinado período de tempo com a amostra estudada. O número de observações pode ser calculado como na amostragem aleatória simples e o intervalo sistemático pode ser arbitrado à partir da freqüência esperada do evento estudado.
a) Seleccione amostras com base nas indicações dadas nas aulas.
Amostragem Aleatória
Fonte: http://www.lee.dante.br/pesquisa/amostragem/planoamostral.html
Amostragem Sistemática
Fonte:http://www.lee.dante.br/pesquisa/amostragem/planoamostral.html
Amostragem Sistemática- Deve obedecer o mesmo princípio da amostragem aleatória simples de iguais probabilidades de pertencer à amostra para todos os componentes da população estudada. No entanto, prevê a coleta de dados ao longo de um período de tempo e arbitra um ritmo para tomada de unidades da população para compor a amostra. Por exemplo, numa listagem de indivíduos da população, sorteamos um nome entre os dez primeiros da lista. A partir do nome sorteado, selecionamos um a cada dez indivíduos (o décimo, vigésimo e assim por diante). A aleatoriedade só está garantida se a apresentação de casos for também aleatória (exemplo: numa população de atendimentos médicos ambularoriais toma-se para amostra 1 em cada 10 pessoas que se apresentam para consulta médica. A amostra será aleatória se a apresentação de pacientes puder ser assumida como igualmente aleatória).
A amostragem sistemática é utilizada quando se quer planejar um período de tempo para execução da coleta de dados ou quando se deseja cobrir um determinado período de tempo com a amostra estudada. O número de observações pode ser calculado como na amostragem aleatória simples e o intervalo sistemático pode ser arbitrado à partir da freqüência esperada do evento estudado.
a) Seleccione amostras com base nas indicações dadas nas aulas.
Amostragem Aleatória
Fonte: http://www.lee.dante.br/pesquisa/amostragem/planoamostral.html
Amostragem Sistemática
C.6 - Índice de Gini e Curva de Lorenz
Curva de Lorenz - A Curva de Lorenz é um gráfico utilizado para representar a distribuição relativa de uma variável em um domínio determinado. O domínio pode ser o conjunto de pessoas de uma região ou país, por exemplo. A variável cuja distribuição se estuda pode ser a renda das pessoas. A curva é traçada considerando-se a percentagem acumulada de pessoas no eixo das abcissas e a percentagem acumulada de renda no eixo das ordenadas.
Esta curva foi desenvolvida pelo economista estadonidense Max O. Lorenz em 1905 para representar a distribuição de renda.
Fonte: http://pt.wikipedia.org/wiki/Curva_de_Lorenz
Índice de Gini - O índice ou coeficiente de Gini é uma medida de concentração ou desigualdade. É comumente utilizada para calcular a desigualdade da distribuição de renda. O índice de Gini aponta a diferença entre os rendimentos dos mais pobres e dos mais ricos. Numericamente, varia de "0 a 1", onde o zero corresponde a completa igualdade de renda, ou seja, todos têm a mesma renda e 1 que corresponde à completa desigualdade, isto é, uma só pessoa detém toda riqueza, e as demais nada tem.
Fonte: http://www.carlosescossia.com/2009/06/o-que-e-indice-de-gini.html
a) Contrua uma curva de Lorenz para cada uma das empresas.
Empresa A
Empresa B
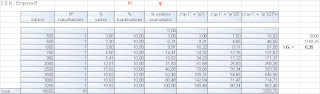
b) Calcule o Índice de Gini para cada uma das empresas.
Empresa A
Empresa B
c) Contrua um gráfico com as duas curvas de Lorenz.
Esta curva foi desenvolvida pelo economista estadonidense Max O. Lorenz em 1905 para representar a distribuição de renda.
Fonte: http://pt.wikipedia.org/wiki/Curva_de_Lorenz
Índice de Gini - O índice ou coeficiente de Gini é uma medida de concentração ou desigualdade. É comumente utilizada para calcular a desigualdade da distribuição de renda. O índice de Gini aponta a diferença entre os rendimentos dos mais pobres e dos mais ricos. Numericamente, varia de "0 a 1", onde o zero corresponde a completa igualdade de renda, ou seja, todos têm a mesma renda e 1 que corresponde à completa desigualdade, isto é, uma só pessoa detém toda riqueza, e as demais nada tem.
Fonte: http://www.carlosescossia.com/2009/06/o-que-e-indice-de-gini.html
a) Contrua uma curva de Lorenz para cada uma das empresas.
Empresa A
Empresa B
b) Calcule o Índice de Gini para cada uma das empresas.
Empresa A
Empresa B
c) Contrua um gráfico com as duas curvas de Lorenz.
C.4 - Piramide etária, estatísticas de sumário e índices demográficos. População residente em Portugal, em 2007, por idades e sexo
a) Elabore a pirâmide etária. Interprete os resultados
Analisando o a pirâmide etária verifica-se que o número de homens como o numero
de mulheres é equilibrada, ou seja, verifica-se tal acontecimento
na faixa etária adulta e criança em ambos os sexos.
O mesmo não acontece com a população idosa porque, o número
de mulheres é superior ao número de homens e pode-se concluir
que a Esperança Média de Vida do sexo feminino é mais elevada.
b) Calcule "Estatísticas de Sumário" para a população residente em Portugal (HM, H e M), em 2007.
c) Calcule os seguintes índices demográficos.
Indice de dependencia total
Indice de dependencia de jovens
Indice de dependencia de idosos
Indice de envelhecimento
Indice de juventude
Indice de juventude da população activa
Indice de longividade
Indice de renovação da população em idade activa
Indice de sustentabilidade potencial
Relação de masculinidade
Analisando o a pirâmide etária verifica-se que o número de homens como o numero
de mulheres é equilibrada, ou seja, verifica-se tal acontecimento
na faixa etária adulta e criança em ambos os sexos.
O mesmo não acontece com a população idosa porque, o número
de mulheres é superior ao número de homens e pode-se concluir
que a Esperança Média de Vida do sexo feminino é mais elevada.
b) Calcule "Estatísticas de Sumário" para a população residente em Portugal (HM, H e M), em 2007.
c) Calcule os seguintes índices demográficos.
Indice de dependencia total
Indice de dependencia de jovens
Indice de dependencia de idosos
Indice de envelhecimento
Indice de juventude
Indice de juventude da população activa
Indice de longividade
Indice de renovação da população em idade activa
Indice de sustentabilidade potencial
Relação de masculinidade
C.3 - Gráficos. Evolução da população residente em Portugal, 1861 a 2007
a) Elabore um gráfico de linha e um gráfico de área.
Gráfico de Linha ( variável X qualitativa).
Gráfico de Linha ou Dispersão (Variável X Quantitativa).
Gráfico de Área.
Gráfico de Linha ( variável X qualitativa).
Gráfico de Linha ou Dispersão (Variável X Quantitativa).
Gráfico de Área.
sábado, 2 de janeiro de 2010
Subscrever:
Mensagens (Atom)